一、介绍

这题看似简单的回溯，却有很多边界问题，足足搞了3-4个小时才通过。

二、题目

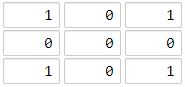
n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

上图为 8 皇后问题的一种解法。

给定一个整数 n，返回所有不同的 n 皇后问题的解决方案。

每一种解法包含一个明确的 n 皇后问题的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例：

输入：4
输出：[
 [".Q..",  // 解法 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // 解法 2
  "Q...",
  "...Q",
  ".Q.."]
]
解释: 4 皇后问题存在两个不同的解法。

提示：

• 皇后彼此不能相互攻击，也就是说：任何两个皇后都不能处于同一条横行、纵行或斜线上。

\n

三、代码

class Solution {

        private int[][] arr;

        private List<List<String>> ans = new ArrayList<>();

        private int n;
        private int countQ = 0;


        public List<List<String>> solveNQueens(int n) {
            this.n = n;
            arr = new int[n + 2][n + 2];
            for (int i = 0; i < n; i++) {
                dg(1, i + 1);
                arr[1][i + 1] = 0;
                countQ--;
            }
            return ans;
        }

        private void dg(int x, int y) {
            arr[x][y] = 1;
            countQ++;
            if (validate(x, y)) {
                if (countQ == n) {
                    output();
                    return;
                }
                if (x < n) {
                    x++;
                    for (int i = 0; i < n; i++) {
                        y = i + 1;
                        dg(x, y);
                        arr[x][y] = 0;
                        countQ--;
                    }
                }
            }
        }

        private void output() {
            ArrayList<String> strings = new ArrayList<>();
            for (int i = 0; i < n; i++) {
                StringBuilder builder = new StringBuilder();
                for (int j = 0; j < n; j++) {
                    builder.append(arr[i + 1][j + 1] == 1 ? "Q" : ".");
                }
                strings.add(builder.toString());
            }
            ans.add(strings);
        }

        private boolean validate(int x, int y) {
            int countXQ = 0;
            int countYQ = 0;
            int countLUQ = 0;
            int countRDQ = 0;
            int countRUQ = 0;
            int countLDQ = 0;
            for (int i = 0; i < n; i++) {
                if (arr[x][i + 1] == 1) {
                    countYQ++;
                }
                if (arr[i + 1][y] == 1) {
                    countXQ++;
                }
                if (x - i > 0 && y - i > 0 && arr[x - i][y - i] == 1) {
                    countLUQ++;
                }
                if (x + i <= n && y + i <= n && arr[x + i][y + i] == 1) {
                    countRDQ++;
                }
                if (x - i > 0 && y + i <= n && arr[x - i][y + i] == 1) {
                    countRUQ++;
                }
                if (x + i <= n && y - i > 0 && arr[x + i][y - i] == 1) {
                    countLDQ++;
                }

            }
            if (countXQ > 1
                    || countYQ > 1
                    || countLUQ > 1
                    || countRDQ > 1
                    || countRUQ > 1
                    || countLDQ > 1
            ) {
                return false;
            }
            return true;
        }
    }