思路

116题还能通过画图看出规律，但这是升级版，非完美二叉树。这题很容易想到用层次遍历，但是是中等难度，肯定不是最优解。

分析下，层次遍历时间复杂度O(N)，已经做到极致了。那么只能从空间复杂度下手，层次遍历空间复杂度为O(N)，如果不存副本，倒是可以优化。

遍历某一层时，就将下一层串起来，这样下一层就可以直接遍历，不用存到队列里。第一层没有上一层，但第一层只有root节点，不需要串起来。

题目

给定一个二叉树

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

进阶：

• 你只能使用常量级额外空间。
• 使用递归解题也符合要求，本题中递归程序占用的栈空间不算做额外的空间复杂度。

示例：

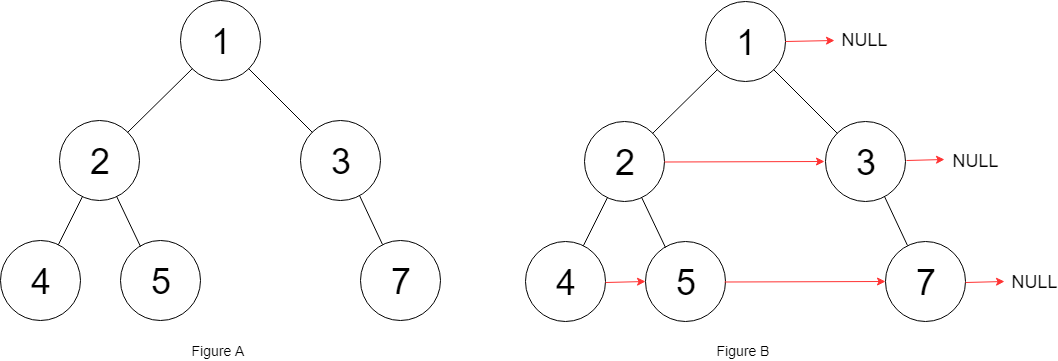
输入：root = [1,2,3,4,5,null,7]
输出：[1,#,2,3,#,4,5,7,#]
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化输出按层序遍历顺序（由 next 指针连接），'#' 表示每层的末尾。

提示：

• 树中的节点数小于 6000
• -100 <= node.val <= 100

代码

    class Solution {

        /**
         * 下一层的头结点
         */
        private Node nextRowHead;
        /**
         * 下一层的尾结点
         */
        private Node nextRowTail;

        public Node connect(Node root) {
            if (root == null) {
                return root;
            }
            Node curr = root;

            do {
                // 内层循环结束后curr为null，但第一次进来时不需要赋值，此时为root
                if (curr == null) {
                    // 从下一行的头结点开始遍历
                    curr = nextRowHead;
                    nextRowHead = null;
                }

                do {
                    buildNextRow(curr.left);
                    buildNextRow(curr.right);
                    curr = curr.next;
                    // 当前层的下一个节点
                } while (curr != null);
                // 下一层
            } while (nextRowHead != null);
            return root;
        }

        /**
         * 将下一层的节点串起来
         */
        private void buildNextRow(Node node) {
            if (node != null) {
                if (nextRowHead == null) {
                    nextRowHead = node;
                    nextRowTail = node;
                } else {
                    nextRowTail.next = node;
                    nextRowTail = node;
                }
            }
        }
    }